图形拟合（二）：多边形拟合

算法

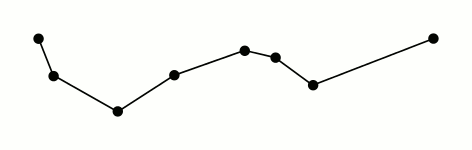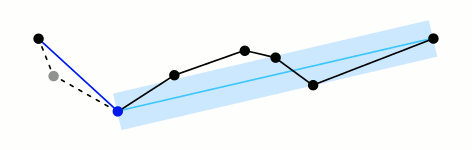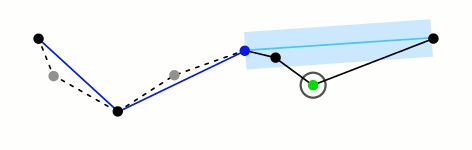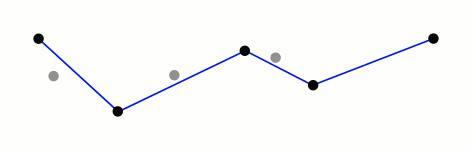
使用拉默-道格拉斯-普克演算法（Ramer–Douglas–Peucker algorithm），对应的解析可以参考：

https://en.wikipedia.org/wiki/Ramer%E2%80%93Douglas%E2%80%93Peucker_algorithm

在OpenCV中也有实现，对应 approxPolyDP 函数。用法可以参考：

https://www.cnblogs.com/k1412/p/6884484.html

JavaScript版本实现

class Point {
  x : number
  y : number
  constructor(_x : number, _y : number) {
    this.x = _x
    this.y = _y
  }
}

class Range {
  start : number
  end : number
  constructor(_start : number, _end : number) {
    this.start = _start
    this.end = _end
  }
}

class MiniOpenCV {

  static approxPolyDP_(
    src_contour : Point[],
    count0 : number,
    dst_contour : (Point | any)[],
    is_closed0 : boolean,
    eps : number,
    _stack : (Range | any)[]
  ): number {
    let init_iters = 3;
    let slice = new Range(0, 0);
    let right_slice = new Range(0, 0);
    let start_pt = new Point(-1000000, -1000000)
    let end_pt = new Point(0, 0);
    let pt = new Point(0, 0);
    let i = 0, j, pos = 0, wpos, count = count0, new_count = 0;
    let is_closed = is_closed0;
    let le_eps = false;
    let top = 0, stacksz = _stack.length;
    let stack = _stack;

    const PUSH_SLICE = (slice : Range) => {
      if (top >= stacksz) {
        stacksz = Math.ceil(stacksz * 3 / 2);
        stack.length = stacksz;
      }
      stack[top++] = JSON.parse(JSON.stringify(slice))
    }

    const READ_PT = (pos : number): [Point, number] => {
      const pt = src_contour[pos];
      if ((++ pos) >= count) {
        pos = 0;
      }
      return [pt, pos]
    }

    const READ_DST_PT = (pos : number): [Point, number] => {
      const pt = dst_contour[pos]
      if ((++ pos) >= count) {
        pos = 0;
      }
      return [pt, pos]
    }

    const WRITE_PT = (pt : Point) => {
      dst_contour[new_count++] = JSON.parse(JSON.stringify(pt));
    }

    if (count === 0) {
      return 0;
    }

    eps *= eps;

    if (!is_closed) {
      right_slice.start = count;
      end_pt = src_contour[0];
      start_pt = src_contour[count - 1];

      if (start_pt.x != end_pt.x || start_pt.y != end_pt.y) {
        slice.start = 0;
        slice.end = count - 1;
        PUSH_SLICE(slice);
      } else {
        is_closed = true;
        init_iters = 1;
      }
    }

    if (is_closed) {
      // 1. Find approximately two farthest points of the contour
      right_slice.start = 0;

      for (i = 0; i < init_iters; i++) {
        let dist, max_dist = 0;
        pos = (pos + right_slice.start) % count;
        [start_pt, pos] = READ_PT(pos);


        for (j = 1; j < count; j++) {
          let dx, dy;

          [pt, pos] = READ_PT(pos);

          dx = pt.x - start_pt.x;
          dy = pt.y - start_pt.y;

          dist = dx * dx + dy * dy;

          if (dist > max_dist) {
            max_dist = dist;
            right_slice.start = j;
          }
        }

        le_eps = max_dist <= eps;
      }

      // 2. initialize the stack
      if (!le_eps) {
        right_slice.end = slice.start = pos % count;
        slice.end = right_slice.start = (right_slice.start + slice.start) % count;

        PUSH_SLICE(right_slice);
        PUSH_SLICE(slice);
      } else {
        WRITE_PT(start_pt);
      }
    }

    // 3. run recursive process
    while (top > 0) {
      slice = stack[--top];
      end_pt = src_contour[slice.end];
      pos = slice.start;
      [start_pt, pos] = READ_PT(pos);

      if (pos != slice.end) {
        let dx, dy, dist, max_dist = 0;

        dx = end_pt.x - start_pt.x;
        dy = end_pt.y - start_pt.y;

        while (pos != slice.end) {
          [pt, pos] = READ_PT(pos);

          dist = Math.abs((pt.y - start_pt.y) * dx - (pt.x - start_pt.x) * dy);

          if (dist > max_dist) {
            max_dist = dist;
            right_slice.start = (pos + count-1) % count;
          }
        }

        le_eps = max_dist * max_dist <= eps * (dx * dx + dy * dy);
      } else {
        le_eps = true;
        // read starting point
        start_pt = src_contour[slice.start];
      }

      if (le_eps) {
        WRITE_PT(start_pt);
      } else {
        right_slice.end = slice.end;
        slice.end = right_slice.start;
        PUSH_SLICE(right_slice);
        PUSH_SLICE(slice);
      }
    }

    if (!is_closed) {
      WRITE_PT(src_contour[count - 1]);
    }

    // last stage: do final clean-up of the approximated contour -
    // remove extra points on the [almost] straight lines.
    is_closed = is_closed0;
    count = new_count;
    pos = is_closed ? count - 1 : 0;
    [start_pt, pos] = READ_DST_PT(pos);

    wpos = pos;
    [pt, pos] = READ_DST_PT(pos);


    let t = Number(!is_closed);

    for (i = t; i < count - t && new_count > 2; i++) {
      let dx, dy, dist, successive_inner_product;
      [end_pt, pos] = READ_DST_PT(pos);


      dx = end_pt.x - start_pt.x;
      dy = end_pt.y - start_pt.y;
      dist = Math.abs((pt.x - start_pt.x) * dy - (pt.y - start_pt.y) * dx);
      successive_inner_product = (pt.x - start_pt.x) * (end_pt.x - pt.x) +
      (pt.y - start_pt.y) * (end_pt.y - pt.y);

      if (dist * dist <= 0.5 * eps * (dx * dx + dy * dy) && dx != 0 && dy != 0 && successive_inner_product >= 0) {
        new_count--;
        dst_contour[wpos] = start_pt = end_pt;
        if ((++wpos) >= count) {
          wpos = 0;
        }
        [pt, pos] = READ_DST_PT(pos);

        i++;
        continue;
      }
      dst_contour[wpos] = start_pt = pt;
      if (++wpos >= count) wpos = 0;
      pt = end_pt;
    }

    if (!is_closed) {
      dst_contour[wpos] = pt;
    }

    return new_count;
  }

  static approxPolyDP(_curve: Point[], epsilon: number, closed: boolean) {
    if (epsilon < 0.0 || !(epsilon < 1e30)) {
      console.error("Epsilon not valid.");
    }
    let npoints = _curve.length;
    if (!npoints) {
      return {
        points: [],
        count: 0
      }
    }
    let _stack = new Array(npoints)
    let _buf = new Array(npoints)
    let nout = MiniOpenCV.approxPolyDP_(_curve, npoints, _buf, closed, epsilon, _stack);
    return {
      points: _buf.filter((p: Point) => !!p),
      count: nout
    };
  }