贝塞尔曲线分段切割与控制点反推
1. 计算贝塞尔线上插值点
这里以二次贝塞尔为例,三次贝塞尔算法类似。根据二次贝塞尔的插值公式,可得该段贝塞尔曲线任意插值点坐标的计算公式为:
$$P_{ratio} = (1 – ratio) ^ 2 * P_{begin} + 2 * ratio * (1 – ratio) * P_{control} + ratio ^ 2 * P_{end} $$
其中,$P_{begin}$ 为贝塞尔曲线起始点,$P_{end}$ 为贝塞尔曲线结束点,$P_{control}$ 为贝塞尔曲线的控制点,$ratio$ 为插值位置的比例,$P_{ratio}$ 为插值位置的实际点坐标。
const calcLinePoint = (ratio: number, bgnP: LinePoint, ctrlP: LinePoint, endP: LinePoint) => {
let res = { x: 0, y: 0, w: 1 };
let factor1 = (1 - ratio) * (1 - ratio);
let factor2 = 2 * ratio * (1 - ratio);
let factor3 = ratio * ratio;
res.x = factor1 * bgnP.x + factor2 * ctrlP.x + factor3 * endP.x;
res.y = factor1 * bgnP.y + factor2 * ctrlP.y + factor3 * endP.y;
return res;
}2. 反推贝塞尔控制点
由(1)中可得,若已知 $ratio$,$P_{ratio}$,$P_{begin}$,$P_{end}$四个参数的值,是可以反推出当前贝塞尔曲线的控制点坐标 $P_{control}$,具体的公式为:
$$P_{control} = (P_{ratio} – ratio ^ 2 * P_{end} – (1 – ratio) ^ 2 * P_{begin}) / (2 * ratio * (1 – ratio))$$
const calcCtrlPoint = (ratio: number, bgnP: LinePoint, lineP: LinePoint, endP: LinePoint) => {
let res = { x: 0, y: 0, w: 1 };
let factor1 = (1 - ratio) * (1 - ratio);
let factor2 = 2 * ratio * (1 - ratio);
let factor3 = ratio * ratio;
res.x = (lineP.x - factor3 * endP.x - factor1 * bgnP.x) / (factor2);
res.y = (lineP.y - factor3 * endP.y - factor1 * bgnP.y) / (factor2);
return res;
}3. 贝塞尔分段切割算法
基于(1)和(2)中的算法,那就可以做到切割任意贝塞尔曲线后,除切割区域外的剩余贝塞尔曲线的位置保持与原来的一致。具体思路如下:
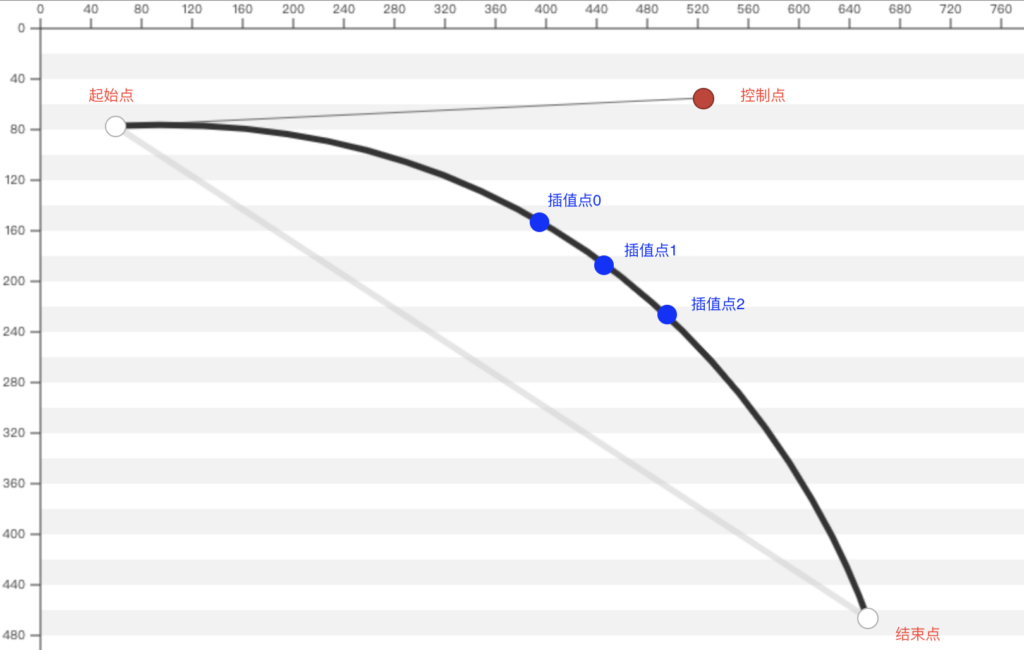
待分段的贝塞尔曲线,假设此时有相邻 插值点 0,插值点1,插值点2 三个点,并有原始的 起始点、结束点、控制点。
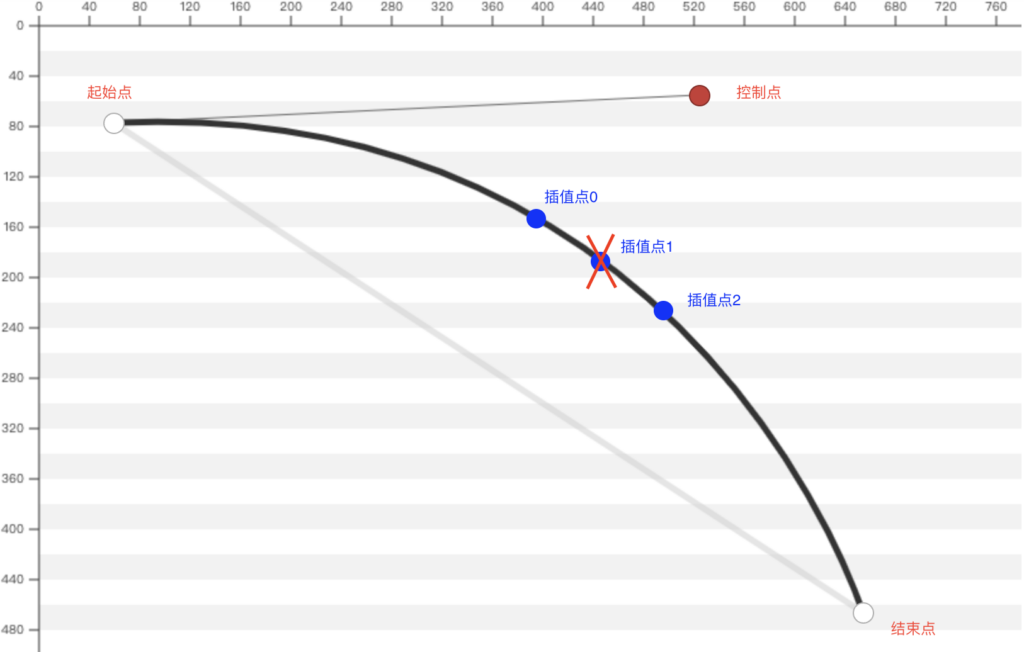
假设此时切割区域为 插值点0 至 插值点2 之间的区域,插值点1 将被移除。移除后需要保证 起始点 – 插值点0,插值点2 – 结束点 这两段贝塞尔曲线的样式不变。具体的方法是:
根据公式(1)分别计算出原贝塞尔曲线上位于 起始点 – 插值点0,插值点2 – 结束点 这两段曲线的插值点,命名为 插值点3 和 插值点4;
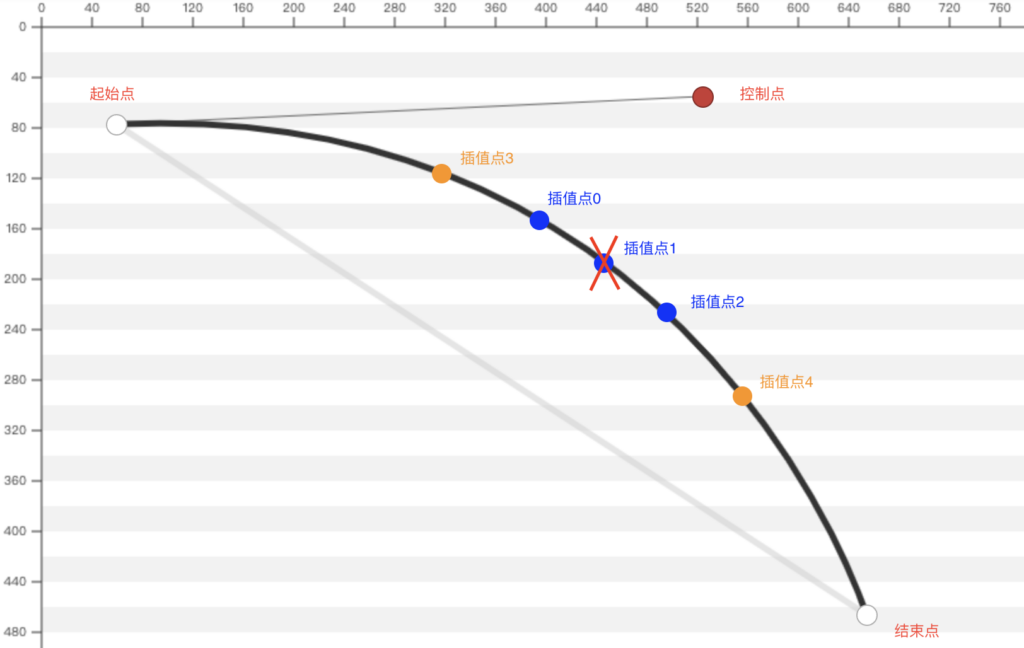
分别计算 插值点3 和 插值点4 在新曲线上的比例,比如若 插值点0 在原曲线的0.45位置,插值点3 在原曲线的0.30位置,那么 插值点3 在 起始点 – 插值点0 这段新曲线的比例位置为 0.3 / 0.45 = 0.66;同理,若 插值点2 在原曲线的0.55位置,插值点4 在原曲线的0.70位置,那么 插值点4 在 插值点2 – 结束点 这段新曲线的比例位置为 (0.7 – 0.55) / (1 – 0.55) = 0.33;
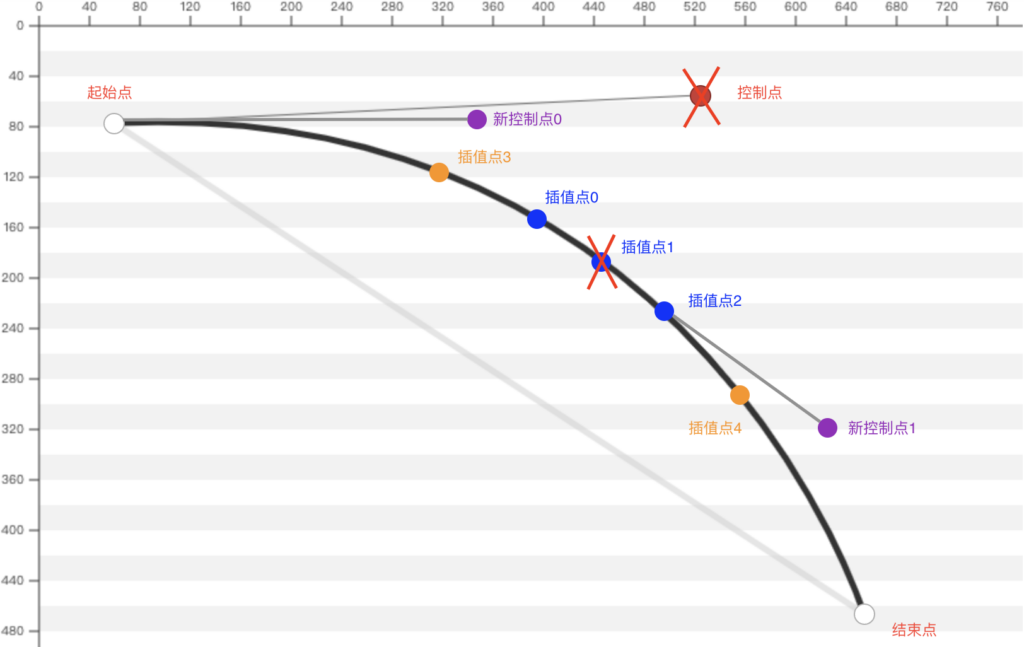
根据 起始点,插值点0,插值点3 及其插值比例位置(0.66)可以利用公式(2)推出 新控制点0;同理,根据 插值点2,结束点,插值点4 及其插值比例位置(0.33)可以推出 新控制点1;
两段新曲线可以通过3中计算得到的点正确绘制,实现最终效果;
具体实现代码如下:
export const splitLine = (points: LinePoint[], erasures: any, radius: number) => {
// 假设此时lines的内容是 线上点,控制点 交替保存,即形如 [A, B, M1, C, M2, D, M3, E, F]
const fittingLine = [];
// 插值点数量
const INTERPOLATION_COUNT = 20;
let impactResult = false; // 用来判断是否有碰撞过,有碰撞过,则说明线条有拆分
const isImpact = function(pointX: any, pointY: any) {
let isImpact = false;
for (let index = 0; index < erasures.length; index++) {
const erasure = erasures[index];
// checkCollision用于检查是否碰撞
isImpact = checkCollision(pointX, pointY, erasure.x, erasure.y, radius);
if (isImpact) {
break;
}
}
if (!impactResult) { // 如果没有碰撞过
impactResult = isImpact;
}
return isImpact;
}
// 曲线仅有一个点
if (points.length === 1) {
return {newLines: [], impactResult: true};
}
// 曲线有两个点
if (points.length === 2) {
// 求出这两个点连线上的点
const dy = (points[1].y - points[0].y);
const dx = (points[1].x - points[0].x);
if (dx === 0 && dy === 0) {
return {newLines: [], impactResult: true};
}
const newLines = []; // 新的线
let flag = true;
let needReverse = dx < 0;
for (let x = points[0].x; needReverse ? x >= points[1].x : x <= points[1].x; needReverse ? x-- : x++) {
let isOrigin = 0; // 是否是原始点(收尾是原始点)
let originSeq;
if (x === points[0].x) {
isOrigin = 1;
originSeq = points[0].originSeq;
} else if(x === points[1].x) {
isOrigin = 1;
originSeq = points[1].originSeq;
}
const fittingPoint = {
x: x,
y: dy * (x - points[0].x) / dx + points[0].y,
}
if (isImpact(fittingPoint.x, fittingPoint.y)) {
impactResult = true;
flag = true;
} else {
if (flag) {
fittingPoint.timestamp = getTimeStamp();
newLines.push([fittingPoint]);
} else {
if (newLines.length > 1) {
newLines[newLines.length - 1].pop()
}
fittingPoint.timestamp = getTimeStamp();
newLines[newLines.length - 1].push(fittingPoint);
}
flag = false;
}
}
return {newLines, impactResult};
}
/* 1. 直线按贝塞尔算法算出点 */
// 点数量必定为奇数
for (let i = 0, len = points.length; i < len - 2; i += 2) {
const bgnP = points[i];
const ctrlP = points[i + 1];
const endP = points[i + 2]; // 是中点
fittingLine.push({
...bgnP,
isOrigin: 1,
ctrlP: {...ctrlP, isOrigin: 1}
});
for (let t = 1; t < INTERPOLATION_COUNT; t++) {
fittingLine.push({
...calcLinePoint(t / INTERPOLATION_COUNT, bgnP, ctrlP, endP),
isOrigin: 0,
ratioPos: t
})
}
if (i === len - 3) {
fittingLine.push({
...endP,
isOrigin: 1,
ctrlP: null
})
}
}
/* 2. 划分线段 */
const newLines = [];
let isPrevPointOmit = true;
let lineLen = 0;
for (const p of fittingLine) {
// 忽略被擦除的点
if (isImpact(p.x, p.y)) {
isPrevPointOmit = true;
} else {
if (isPrevPointOmit) {
newLines.push([p]);
lineLen++;
} else {
newLines[lineLen - 1].push(p);
}
isPrevPointOmit = false;
}
}
/* 3. 重新计算控制点 */
const resNewLines = [];
for (let line of newLines) {
const fmtLine = [];
const len = line.length;
for (let i = 0; i < len; i++) {
const p:any = line[i];
if (p.isOrigin) {
fmtLine.push({
x: p.x,
y: p.y,
})
if (p.ctrlP) {
fmtLine.push(p.ctrlP);
}
}
}
if (!(line[0].isOrigin === 1)) {
// 如果线段开头不是原有的线上点,则需要加一个开始点和一个控制点
const headPoint = line[0];
const endPos = line.findIndex((el) => el.isOrigin);
// 如果新线上有原来的点
if (endPos !== -1) {
const oriPoint = line[endPos];
let ctrlPoint = null;
// 如果是最后一个插值点
if (headPoint.ratioPos === INTERPOLATION_COUNT - 1) {
ctrlPoint = {
x: (headPoint.x + oriPoint.x) / 2,
y: (headPoint.y + oriPoint.y) / 2,
}
} else {
const newRatio = 1 - 1 / endPos;
const linePoint = line[endPos - 1];
ctrlPoint = calcCtrlPoint(newRatio, headPoint, linePoint, oriPoint);
}
fmtLine.unshift(ctrlPoint);
fmtLine.unshift(headPoint);
} else {
// 如果线上没有原来的点,则认为这是一条彻底的新线
const tailPoint = line[len - 1];
const newLineLen = tailPoint.ratioPos - headPoint.ratioPos + 1;
if (newLineLen === 1) {
fmtLine.push(headPoint);
} else if (newLineLen === 2) {
fmtLine.push(headPoint);
fmtLine.push(tailPoint);
} else {
const newRatio = 1 - 1 / newLineLen;
const ctrlPoint = calcCtrlPoint(newRatio, headPoint, line[len - 2], tailPoint)
fmtLine.push(headPoint);
fmtLine.push(ctrlPoint);
fmtLine.push(tailPoint);
}
continue;
}
}
if (!(line[len - 1].isOrigin === 1)) {
// 如果线段结尾不是原有的线上点,移除最后一个控制点,加一个新控制点和结束点
fmtLine.pop();
let startPos = -1;
for (let i = len - 1; i >= 0; i--) {
const el = line[i];
if (el.isOrigin) {
startPos = i;
break;
}
}
if (startPos !== -1) {
const tailPoint = line[len - 1];
const oriPoint = line[startPos];
let ctrlPoint = null;
// 如果是第一个插值点
if (tailPoint.ratioPos === 1) {
ctrlPoint = {
x: (tailPoint.x + oriPoint.x) / 2,
y: (tailPoint.y + oriPoint.y) / 2,
}
} else {
const newRatio = 1 - 1 / tailPoint.ratioPos;
const linePoint = line[len - 2];
ctrlPoint = calcCtrlPoint(newRatio, oriPoint, linePoint, tailPoint);
}
fmtLine.push(ctrlPoint);
fmtLine.push(tailPoint);
} else {
// 如果线上没有原来的点,则认为这是一条彻底的新线,与先前判断重复,不再处理
}
}
// 如果新线的终止点在原线上,抛弃终止点的控制点(若有)
if (line[len - 1].isOrigin && line[len - 1].ctrlP) {
fmtLine.pop();
}
resNewLines.push(fmtLine.map(({x, y, w, isOrigin, originSeq, middle}) =>
({x: +(x.toFixed(4)), y: +(y.toFixed(4))})
));
}
/* 4. 返回新线段 */
return {newLines: resNewLines, impactResult};
}